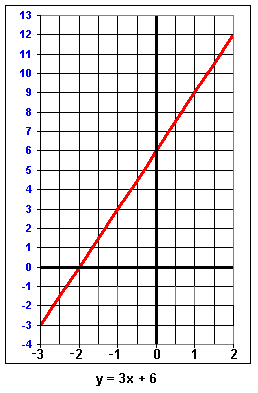
Calculus Primer Calculus Tutorial

Calculus Primer Scroll To The Bottom For Derivative and Integral Calculator

Among other things, calculus involves studying analytic geometry (analyzing graphs). The above graph should be familiar to anyone who has studied elementary algebra. The horizontal axis is the 'X' axis and the vertical axis is the 'Y' axis.

The primary concern of differential calculus is determining slopes of equations. When dealing with a linear (straight line) equation, this is relatively easy. The slope of a line (designated by the letter 'm') is defined as the difference in 'y' divided by the difference in 'x'. (or the "rise over the run" as it is sometimes called).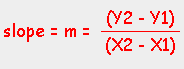

Mathematicians use the Greek letter delta "Δ" to represent "difference" and so this equation could be written: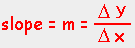

Using y=3x + 6 (the red line in the graph above), we take the 2 points (x=2, y=12) and (x=-2, y=0) and calculate the slope:

There is an easy method to calculate the slope of linear equations.

For equations of the form y = a x + b = 0, the slope equals 'a' (the coefficient of 'x').
This is better than choosing points and calculating differences don't you think ?
Just one more quick example - what is the slope of 5y = -3x + 7 ?
Since the equation has to be of the form y = ax +b then
y = -3/5 x + 7/5 and so the slope = -3/5.

Differential Calculus

In the previous section, we learned how to calculate the slope of a linear equation (equations whose exponents = 1).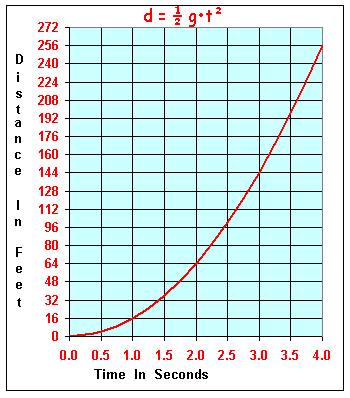
What happens when dealing with quadratic, cubic and higher-power equations?

The graph above is based on a quadratic equation which predicts the distance an object has fallen (the y-axis) in relation to time (the x-axis). You cannot state one specific slope for this equation because the slope is constantly varying. What can be calculated is the slope at any point along the curve. Let's calculate the slope when time = 3 seconds.

The formula states the distance (in feet) = ½ • g • t² (where g = 32 feet/sec²). So, when t = 3 seconds, d= ½ • 32 • 3² = 16 • 9 = 144 feet.
So, we have our first set of values:

y=144 and x=3
But what do we do for choosing a second point? We could try using a value of t= 4 seconds, remembering this is not the same slope at t=3. So, we get:
d= ½• 32 • 4² = 16 • 16 = 256 feet.
Now, we have our second set of values: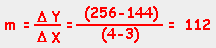
y=256 and x=4 Calculating this approximate slope yields:

Why don't we choose a closer value of x such as 3.1? When that is the case, the distance equals 153.76 feet and our slope is:

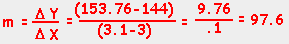
How about choosing a value of x that is even closer to 3 than 3.1 ? Besides representing a difference, Δx (called 'delta x') also represents the smallest possible quantity greater than zero. Δx is less than a millionth, less than a trillionth - it's 1 divided by infinity.
So, when x₂ = 3 + Δx , then y₂ equals
½•g•t² = 16•(3 + Δx)² = 16•(9 + 6Δx + Δx²) = 144 + 96Δx + 16Δx²

and the slope at x = 3 can be calculated as: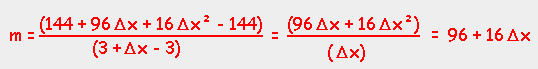

Since Δx is such an incredibly minuscule quantity, we can safely say that at x=3, slope = 96. Incidentally, the process of calculating a slope is called differentiation, the result of these calculations is called the derivative and this branch of mathematics is called differential calculus. The derivative is usually represented by dy/dx or f'(x).

Although the above method does work, it has 2 drawbacks - it is rather cumbersome and it only calculates the slope at one particular point. If we wanted to know the slope at x = 2, we would have to go through all those calculations again. Is there an easier way for determining the slope of an equation at any point? Yes !

Differentiation the Easy Way For a function of the form k • x ⁿ, the derivative is equal to
n • k • x ^(n-1)

A good example is the equation d= ½ • g • T² (or d = 16 • T²) The derivative equals 2 • 16 • T or 32 • T

Having determined the derivative, we can put it to use by the previous example when we calculated the slope for x=3. When x = 3 (or time = 3 seconds), the slope = 32 • 3 or 96. WOW that's a lot easier huh? What about the slope at 2 seconds ? 32 • 2 equals 64.

And what is the purpose of all this slope measuring ? In this equation, every time we determine a slope at a particular point in time, we are calculating velocity. So, at time = 2 seconds, an object has fallen 64 feet and has a velocity of 64 feet per second. When time = 3 seconds, distance = 144 feet and velocity = 96 feet per second.

Just a few more comments. The derivative of a constant (for example the number 7) is always zero. So, by way of example, the derivative of x² + 7 is 2•x. Also, if an equation has more than 1 'x' term, simply differentiate each term and then sum those derivatives.
Example: What is the derivative of 3x³ -5x² + 2x + 13 ?
Answer: 9x² - 10x + 2
One important point to remember is that this method of differentiation works ONLY for equations of the form k • x ⁿ.

Integral Calculus

As we learned, differential calculus involves calculating slopes and now we'll learn about integral calculus which involves calculating areas.

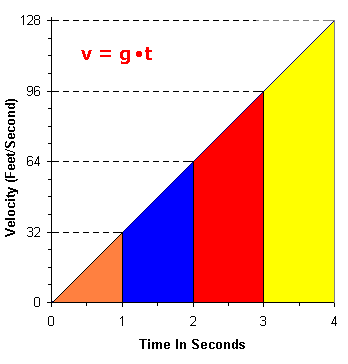
The above graph where velocity = g • T (or v = 32 • T), is based on the derivative of the second graph equation d= ½ • g • t². Now, if we wanted to determine the distance an object has fallen, we calculate the "area under the curve". Yes, the "curve" in this case is a straight line but the principles of integral calculus still apply.

If we calculated the sum of the orange, blue and red areas this would equal the distance fallen after 3 seconds.
Area of a Right Triangle = ½ (base * height)
= ½ (3 seconds * 96 feet per second) = 144 feet
Now looking at the previous graph, we see that this is the precise distance after 3 seconds.
If we wanted to find the distance fallen between 2 and 3 seconds, we calculate ALL the area from 0 to 3 seconds (144 feet)
and then subtract the distance from 0 to 2 seconds:
½ (2 seconds * 64 feet per second) = 64 feet
So, the distance fallen between 2 and 3 seconds is 144 - 64 = 80 feet.
Looking at the previous graph and doing the subtraction, we see the numbers are the same.

So how were we calculating these areas ? We multiplied the y-axis (which is the quantity g • T) by the x-axis (time in seconds or 'T') and we multiplied this by ½ . So we calculated the area by the formula ½ (g • T • T) which equals ½ • g • T², and this is the precise formula which was used in the previous section !!
The process of calculating area is called integration, the resultant formula is called the integral and this branch of mathematics is called integral calculus .
(NOTE: the integral is sometimes called the anti-derivative (not much imagination went into that word huh?)
Is there an easier way to integrate an equation? Darned right !

Integration the Easy Way

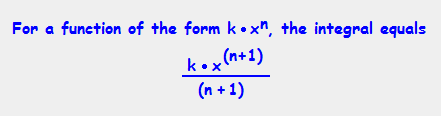
Example 1: What is the integral of 5x² + 3x -7 ?
Answer: (5x³)/3 + (3x²)/2 -7x + c where 'c' is a constant.
Since the derivative of a constant is zero, when calculating an integral we have to allow for a constant.

Example 2: Here's an interesting example of integral calculus.
The area of a sphere is calculated by the formula 4•π•r².
What is the integral (anti-derivative) of this formula?
Answer: (4•π•r³)/3 which is the formula for the volume of a sphere !

Well congratulations !! If you have read this tutorial carefully, you now have a good understanding of calculus (both differential and integral) !! Granted, this was a very quick, "bare bones" explanation, and it represents a very small tip of an incredibly huge "Calculus Iceberg". However, you now understand the "big picture" of what calculus is all about.

As a bonus, the calculator below will help you determine derivatives and integrals.

Derivative and Integral Calculator Only for equations of the form k • x ⁿ

Return To Home Page