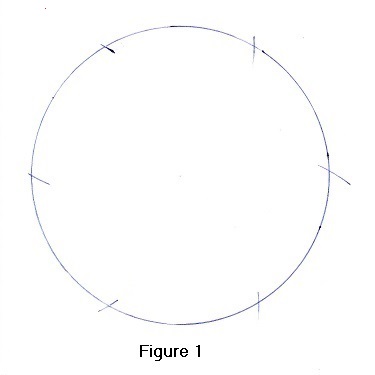The easiest regular polygon to construct is a hexagon.         To construct a hexagon, use a compass to draw a circle. Now, (keeping the compass at the same exact setting), place the compass point on the circumference and strike an arc on the circumference. Next, place the compass point in the arc just drawn and strike another arc. Do this until you have drawn six arcs. (See Figure 1). Now, get a ruler, and draw lines from one arc to the next. The 6 lines you just drew are the sides of the regular hexagon. (See Figure 2). A hexagon is the only case in which a polygon's sides will exactly equal the radius but, by using a compass, a ruler and the calculator below, you can construct regular polygons with any number of sides. Polygon Sides     R a d i u s = Central Angle =   Multiply Radius by Polygon Side =   Click "RESET" to clear all the boxes. I N S T R U C T I O N S Let's say we want to construct a pentagon. Start out by drawing a circle with a compass. (See Figure 3) You do not have to draw the radius, but measure it as precisely as you can. (We measured the radius as 6.70 centimeters.) Using the calculator, we determine the length of each pentagon side (line AB), by entering "polygon sides" 5 , "radius =" 6.70 and then clicking "CALCULATE". The calculator generates 3 numbers. The one we need for this construction is the "polygon side =" number, which equals 7.8765. Now, as precisely as you can, set the compass width for 7.8765 cm (okay, 7.88 cm is more than sufficient), place the compass point at point A and strike an arc at point B. Then continuing from point B, strike another 4 arcs. 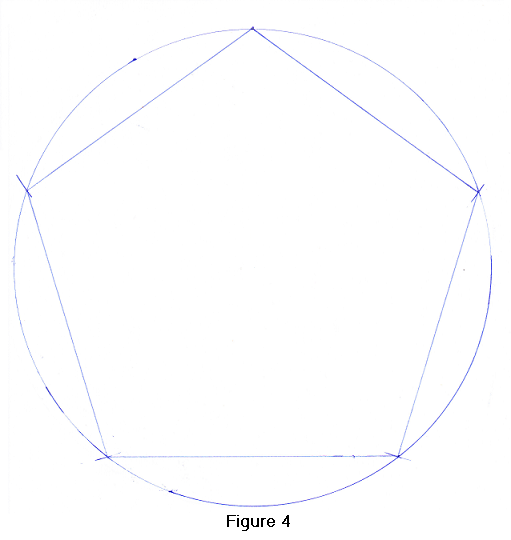Using a ruler, draw the polygon sides from one arc to the next and you have just constructed a regular pentagon! (see Figure 4) Equation Used In This Calculator Let's say you want to construct a pentagon. Start by drawing a circle. Looking at the graphic, we need to calculate how long each side (the red line) is going to be. As precisely as you can, measure the radius. (For this example let's say it is 9.5 cm). From trigonometry, we know that sine (36°) = ½ side ÷ radius ½ side = .58779 × 9.5 ½ side = 5.5840 Therefore, each side = 2 * 5.584 = 11.168 cm And so the equation for calculating the polygon side length is: length = 2 × radius × sine (n) where n = 180° ÷ number of polygon sides