Cramer's Rule

Cramer's Rule for Solving Simultaneous Equations

When solving simultaneous equations (or systems of equations), several methods can be used such as the substitution method or the elimination method. Another system Cramer's Rule, named after the Swiss mathematician Gabriel Cramer (1704-1752) involves placing the coefficients and constants of each equation into determinants.

Solving For Two Unknowns If we have two equations:

ax + by = e
cx + dy = f

we can use Cramer's Rule by putting the 4 coefficients (a, b, c and d) and 2 constants (e & f) into 3 second order determinants. (A second order determinant has 4 numbers arranged in 2 columns by 2 rows.)

The denominator determinant (dn) is created from the coefficients on the left side of the equations.

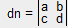
The x determinant's numerator resembles the dn determinant except the 'x' coefficients (a & c) are replaced by the constants (e & f).

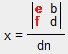
The y determinant's numerator resembles the dn determinant except the 'y' coefficients (b & d) are replaced by the constants (e & f).

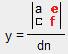
If we were to evaluate these determinants, it would be done based on this procedure:

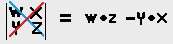
Now that we know Cramer's Rule for 2 unknowns and evaluating determinants, let's solve some equations.
2x + 3y = 12
3x - 4y = 1
From the above instructions, we can see that:
a = 2 b = 3 c =3 d = -4 e = 12 f = 1

dn = (a • d) - (c • b)
dn = (2 • -4) - (3 • 3)
dn = -17

x = [(e • d) - (f • b)] ÷ dn
x = [(12 • -4) - (1 • 3)] ÷ -17
x = 3

y = [(a • f) -(c • e)] ÷ dn
y = [(2 • 1) -(3 • 12)] ÷ -17
y = 2

Cramer's Rule determines the solutions in the two unknown calculator.

Solving For Three Unknowns

For three unknowns, we need to know how to evaluate a third order determinant which is demonstrated in the graphic below.

Solving for three unknowns requires 3 equations:
ax + by + cz = j
dx + ey + fz = k
gx + hy + iz = l

We need to put the 9 coefficients ('a' through 'i') and the 3 constants (j, k and l) into 4 third order determinants
and then evaluate each determinant.

Now that the numbers have been inserted into the determinants, we can now evaluate them.

Now that we have learned about Cramer's Rule for three unknowns, we can solve some equations.

2x + 3y + 4z = 119
5x - 6y + 7z = 80
8x + 9y +10z = 353

We can see that:
a = 2 b = 3 c = 4 d = 5 e = -6 f = 7 g = 8 h = 9 i = 10
j = 119 k = 80 l = 353

dn = (a•e•i) + (b•f•g) + (c•d•h) - (g•e•c) - (h•f•a) - (i•d•b)
dn = (2•-6•10) + (3•7•8) + (4•5•9) - (8•-6•4) - (9•7•2) - (10•5•3)
dn = 144

x=(j•e•i) +(b•f•l)+(c•k•h)-(l•e•c)-(h•f•j)-(i•k•b) ÷ dn
x=[(119•-6•10) +(3•7•353) +(4•80•9)
-(353•-6•4) -(9•7•119) -(10•80•3)] ÷ dn
x = 1,728 ÷ 144 = 12

y = [(a• k• i) + (j• f• g) + (c• d• l) - (g• k• c) - (l• f• a) - (i• d• j)] ÷ dn
y = [(2• 80• 10) + (119• 7 • 8) + (4 • 5 • 353)
- (8 • 80• 4) - (353 • 7• 2) - (10• 5 • 119) ÷ dn
y = 1,872 ÷ 144 = 13

z = [(a• e• l) + (b• k• g) + (j• d• h) - (g• e• j) - (h• k• a) - (l• d• b)] ÷ dn
z = [(2 •-6 •353) + (3• 80• 8) + (119• 5• 9)
- (8• -6• 119) - (9 •80 •2) - (353 •5 •3)] ÷ dn
z = 2,016 ÷ 144 = 14

Cramer's Rule determines the solutions in the three unknown calculator.

Return To Home Page