| | |
|
- Calculus -
Calculating Minimum
| | |

| | |
|
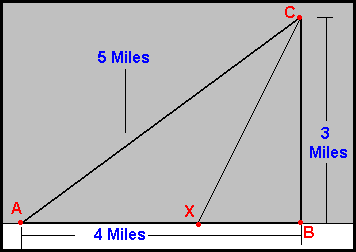
Finally, we will use calculus for a real-world application. The Ajax Water Company (point A), is located along a road (Line AB). You want to run water pipes so you can supply the town of Coolville (point C) with water. Laying pipe parallel to the road (Line AB) is easier and cheaper and costs 1 million dollars per mile. Laying pipe in the gray area is tougher and more expensive (rough terrain, heavily forested, etc) and costs 2.5 million dollars per mile.
| | |
|
The shortest route (but not the cheapest) is AC and is 5 miles but would cost 12.5 million dollars. Laying pipe along route ABC would cost 4 million dollars for 4 miles along Line AB and 7.5 million dollars for 3 miles along Line BC for a total of 11.5 million dollars. There is a route (AXC) that would cost even less than this. Here's how to calculate it.
We must set up an equation for the total cost.
Which Equals: 4 * ($1) - XB*($1) Plus 2.5*(SqRoot (XB2 + 9)) Multiplying and then adding up terms we get: Taking the derivative (by using the Chain Rule): Moving the 1 to the "left side" of the equation: 1= --------------------------------------- 2 * SqRt(6.25 XB2 + 56.25)
Simplifying: 1= ---------------------------------- SqRt(6.25 XB2 + 56.25)
SqRt(6.25 XB2 + 56.25) = 6.25 XB 6.25 XB2 + 56.25 = 39.0625 XB2 32.8125 XB2 -56.25 = 0 XB = 1.3093073414159541 or 1.309 (rounded)
So line AX = 4 - 1.309 miles = 2.691 miles and
|
Copyright © 1999 - 1728 Software Systems