Central Angle
Calculator
Calculates
Arc Length, Radius,
Central Angle
and it calculates sector area
Scroll down for instructions and sample problems.
| |
You will find these 2 graphics helpful when using this calculator, working with central angles, calculating arc lengths, etc.
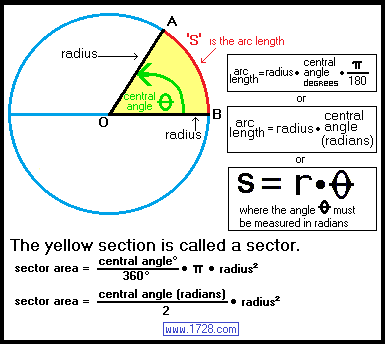
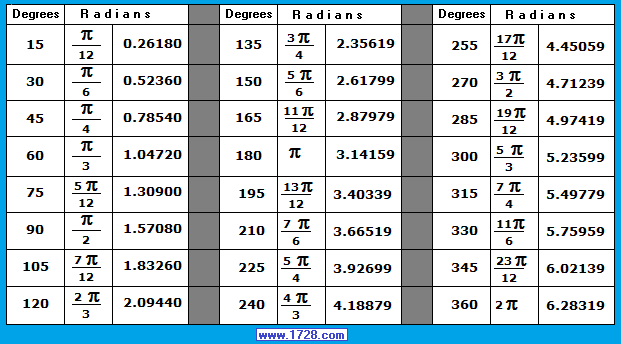
|
This calculator utilizes these equations:
arc length = [radius • central angle (radians)]
arc length = circumference • [central angle (degrees) ÷ 360]
where circumference = [2 • π • radius]
Knowing two of these three variables, you can calculate the third. Even easier, this calculator can solve it for you.
Do you want to solve for
I N S T R U C T I O N S
Start by clicking "Arc Length", "Radius" or "Central Angle".
Enter the 2 lines of data.
Click "CALCULATE" and you have your answer.
Clicking "RESET" clears all of the boxes.
Example Problems
1) A circle has a radius of 7 and a central angle of 2 radians. What is the arc length?
Click the "Arc Length" button, input radius 7 and central angle =2.
Click "CALCULATE" and your answer is 14.
This calculator also accepts input in degrees as well as radians.
For this problem let's try some new data.
1b) Radius = 3.6 central angle 63.8 degrees. Arc Length equals?
Click the "Arc Length" button, input radius 3.6 then click the "DEGREES" button. Enter central angle =63.8 then click "CALCULATE" and your answer is Arc Length = 4.0087.
2) A circle has an arc length of 5.9 and a central angle of 1.67 radians. What is the radius?
Click the "Radius" button, input arc length 5.9 and central angle 1.67.
Click "CALCULATE" and your answer is radius = 3.5329.
Let's try inputting degrees again.
2b) A circle's arc length is 4.9 with a central angle of 123 degrees. What is the radius?
Click the "Radius" button, enter arc length = 4.9 then click the "DEGREES" button. Enter central angle =123 then click "CALCULATE" and your answer is Radius = 2.2825.
3) An angle has an arc length of 2 and a radius of 2. What is the central angle?
Click the "Central Angle" button, input arc length =2 and radius =2.
Click "CALCULATE" and your answer is 1 Radian and 57.296 degrees.
Numbers are displayed in scientific notation with the amount of
significant figures you specify. For easier readability, numbers between .001 and 1,000
will not be in scientific notation but will still have the same precision.
You may change the number of significant figures displayed by
changing the number in the box above.
Most browsers, will display the answers properly but
if you are seeing no answers at all, enter a zero in the box above, which will
eliminate all formatting but at least you will see the answers.
|
|



