Trigonometry

Trigonometry is a word derived from Greek and it means the measurement of triangles. Basically, it is the study of triangles (particularly right triangles) and the relationships between their sides and angles.
If you've just started studying trigonometry (or if you are here for a 'refresher' course), you've probably seen terms such as 'sine' or 'arctangent'. Now you'll see what they mean.

Basic Trigonometric Functions

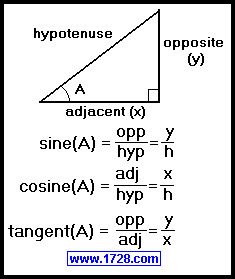The above diagram is a right triangle with sides labeled in terms of Angle A.
(Yes, the hypotenuse is also an "adjacent" side of angle A, but it always gets labeled as hypotenuse. Incidentally, the hypotenuse is always the longest side of a right triangle and it is always opposite the right angle.)

Let's suppose Angle A is 40°. Using the handy trigonometry calculator, we look up the sine of 40° and find that it is 0.64279 but what exactly does this mean? Looking at the definition, we see that the sine of an angle is the ratio of the length of the opposite side divided by the length of the hypotenuse. So, we can say:

sine(40°) = 0.64279 = opposite side ÷ hypotenuse

This means that for every right triangle with a 40° angle, the ratio of the opposite side to the hypotenuse will always be 0.64279.
Let's suppose we have such a triangle and we know that the hypotenuse is 7 feet long. How long is the opposite side?
From above, we showed that 0.64279 = opposite side ÷ hypotenuse. Using a little algebra we can say that the opposite side = 0.64279 • hypotenuse or 0.64279 • 7. Therefore the opposite side = 4.4995 feet.

If we wanted to find the length of the third side, (the adjacent side), we could use the Pythagorean Theorem, but we can solve it using trigonometry.
We see from the above chart that the cosine of angle A = adjacent side ÷ hypotenuse. Using the calculator, we find that the cosine of 40° = 0.76604 and so:

cosine(40°) = 0.76604 = adjacent side ÷ hypotenuse
Using a little algebra, we can say the
adjacent side = 0.76604 • hypotenuse
adjacent side = 0.76604 • 7
adjacent side = 5.3623 feet

Just to make absolutely sure of our calculations (and to have an excuse to show another trigonometric function), we see that the tangent function is the ratio of the opposite side divided by the adjacent side.
In this case the opposite side divided by the adjacent is 4.4995 ÷ 5.3623 which equals 0.83911. Looking up the tangent of 40° on the calculator, shows that it equals 0.8391 which agrees pretty darned well don't you think?

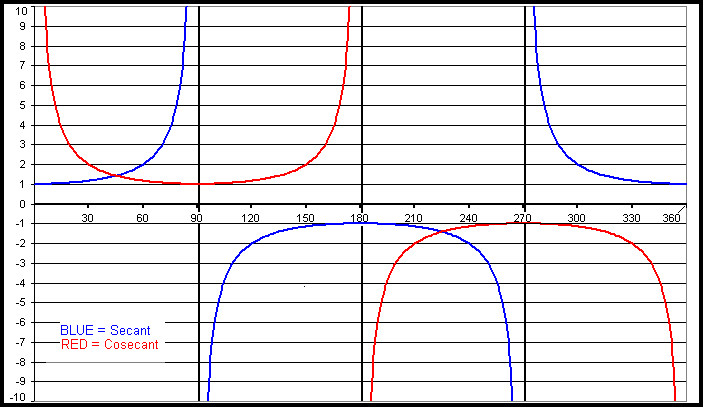
Sine, cosine and tangent are the most frequently used trigonometric functions. There are 3 other functions (cotangent, secant and cosecant) but because this is just an introduction to trigonometry, there is no need to discuss these. (But if you really have to know, you can find the definitions at the calculator as well as other pages).

Angles Measured In Radians

Eventually, in your study of trigonometry, you will encounter the term radian. Like degrees, the radian is a unit of angular measure but unlike degrees, it is not some arbitrary unit that was conveniently chosen.
The radian is the subtended central angle of a circle (∠A) formed by an arc (red line) whose length exactly equals that of the radius. Let's see how this is derived.

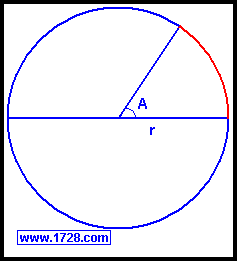
From the formulas for a circle, we see that the

circumference = 2 • π • radius

So, for every circle, 2 π radii subtend a "central angle" of 360°
and therefore one radius would subtend a central angle of
360° ÷ (2 • π) = 180° ÷ π = 57.295779513... degrees = 1 radian

Some of the more common angles expressed in radians are:

180° = π radians     90° = π ÷ 2 radians     60° = π ÷ 3 radians
45° = π ÷ 4 radians     30° = π ÷ 6 radians     20° = π ÷ 9 radians
15° = π ÷ 12 radians     10° = π ÷ 18 radians     5° = π ÷ 36 radians

To convert degrees to radians multiply by (π ÷ 180)
To convert radians to degrees multiply by (180 ÷ π)
Or here's an angle converter that you can use.

The further you progress in mathematics, the more you'll encounter angular measure in radians rather than degrees. You can see the reason since the radian is derived from its relationship to the circle.



Inverse Trigonometric Functions

The term "inverse" is a little deceiving because it implies a reciprocal. To make things even more confusing, the abbreviations for these functions also seem to suggest a reciprocal. For example, the inverse sine function is sin-1 but it does not mean 1 / sine. Okay, let's see what it does mean.

Inverse trigonometric functions are also known as arc functions.
Just as there are 6 trigonometric functions, there are also 6 trigonometric arc functions - arc sine, arc cosine, and so on.
The arc function means the angle whose trigonometric function equals a specific value.
Stating this another way, if the trigonometric function of ∠ y = x, then the arc function of x is ∠ y.
For example, the arc sine of 0.64279 is 40°.

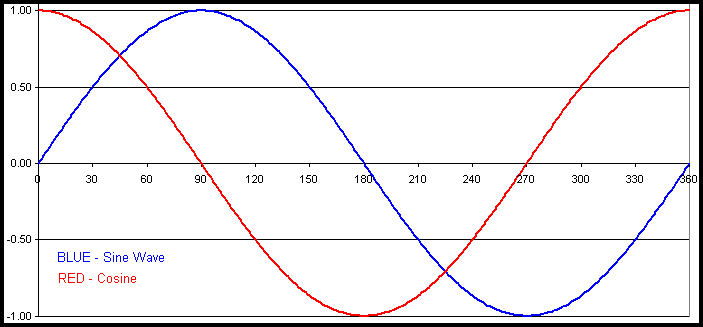
If we graph the trigonometric functions (see below), we see that each of the six trigonometric arc functions can have 2 values.
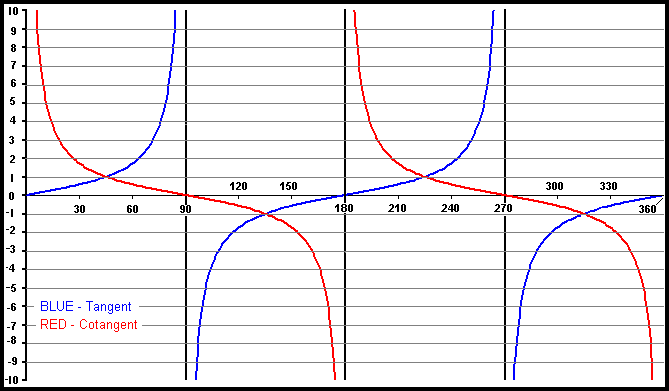
For example, looking at the sine graph we can see that the arc sine of .5 can be 30° or 150°. Looking at the tangent graph, the arc tangent of 1.732 can be 60° or 240°.
We stated above that the arc sine of 0.64279 is 40° but it is also 140°
If we call one arc function value ∠y and we call the second arc function value ∠y2 then we have these 6 formulas for determining the second arc function values:



Graphs of the 6 Trigonometric Functions


Go To Page Two
Solving Oblique Triangles Using Law of Sines and Law of Cosines


Go To Page Three
Solving Oblique Triangles Without Using Law of Sines and Law of Cosines

Return To Home Page

Copyright © 2000   1728 Software Systems