TRIANGULAR PRISM CALCULATOR

Triangular Prism Calculator If you need a Rectangular Prism Calculator, click here.

Input the 3 triangle sides and the height:

A triangular prism is a geometric solid having 2 identical, parallel, triangular bases which are perpindicular to the 3 rectangular faces.
In the above graphic, the green triangle is one of the bases and the red and blue planes are 2 of the 3 faces.
The triangles can be any type of triangle (acute, right or obtuse).
This calculator computes a triangular prism's area and volume when the triangle sides and prism height have been input.
It's great to have a calculator for calculating triangular prisms, but let's see the mathematics of this.

A triangular prism has sides of 5, 6 and 7 with a height of 9.
What is the area and volume of this prism?
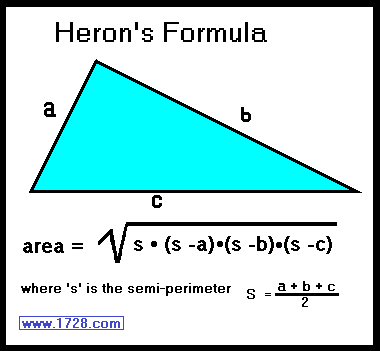
The first thing to do is to calculate the area of the triangular base. Since we know all 3 triangle sides, we will us Heron's Formula.

Semi-Perimeter = (5 + 6 + 7) ÷ 2
Semi-Perimeter = 18 ÷ 2
Semi-Perimeter = 9
Triangle Area = square root [9 * (9-5) * (9-6) * (9-7)]
Triangle Area = square root [9 * 4 * 3 * 2]
Triangle Area = square root (216)
Triangle Area = 14.6969384567
Since a triangular prism has two triangles, the area of both triangles equals
2 * 14.6969384567 = 29.3938769134

Now to calculate the area of the 3 rectangular faces:
Rectangular face area = 9 * (5 + 6 + 7)
Rectangular face area = 162
For the total prism area we add up both areas:
Total Area = 29.3938769134 + 162
Total Area = 191.3938769134

Since we already calculated the triangle area, the volume is easily calculated by:
Volume = triangle area * height
Volume = 14.6969384567 * 9
Volume = 132.2724461103