If some of the terminology used in this calculator seems unfamiliar to you, please read the section below or go to the regular polygon calculator.

Most people think of a prism as a 3-sided object such as the one pictured here.

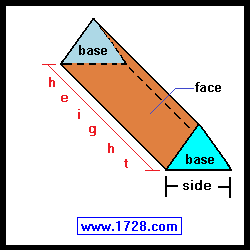This happens to be a right regular prism - a solid geometric figure whose bases are parallel regular polygons and whose faces are all rectangles perpendicular to the bases. (Since the rectangles are perpendicular to the regular polygon bases, you can see why these are called right, regular prisms).
Specifically, the diagram above is a triangular right regular prism because its 2 bases are 3-sided regular polygons (or triangles).
There are also square right regular prisms, pentagonal (pictured below), hexagonal, heptagonal and so on.

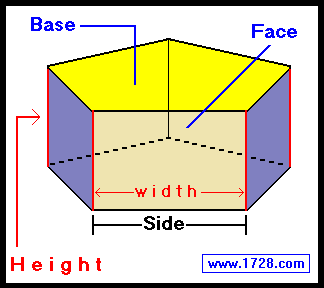
Basically, we can think of a right regular prism as a regular polygon that has been extended 90 degrees into a third dimension - height. In the above diagram, the yellow area is one of the two bases, and the rectangle formed by the 'height edge' and 'side edge' is one of the five faces.

Prism Area = (Height • Width • Number of Sides) + (Area of Both Bases)

Prism Volume = Area of Base • Height

---

Significant Figures >>>

The default setting is for 5 significant figures but you can change that by inputting another number in the box above.

Answers are displayed in scientific notation and for easier readability, numbers between .001 and 1,000 will be displayed in standard format (with the same number of significant figures.)
The answers should display properly but there are a few browsers that will show no output whatsoever. If so, enter a zero in the box above. This eliminates all formatting but it is better than seeing no output at all.

_____________________

Return To Home Page

Copyright © 1999 - 1728 Software Systems