One way to generate a circle's equation, is to fill in the standard form with the center values and its radius. (x -h)² + (y -k)² = radius² 'h' and 'k' are usually used to denote a circle's center.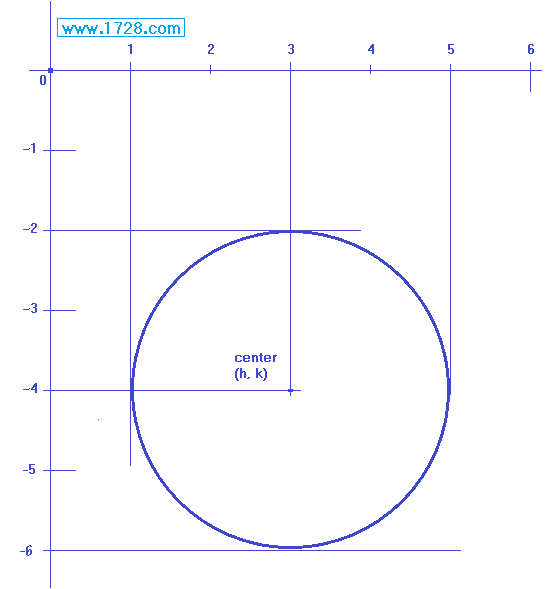 For Example: What is the equation of a circle whose center is (3, -4) and the radius is 2? Filling in this equation: (x -h)² + (y -k)² = radius² we get: (x -3)² + (y - -4)² = 2² which equals (x -3)² + (y +4)² = 4 which is the standard form of the equation If we multiply this, it becomes the general form of the circle's equation. x² -6x + 9 + y² + 8y +16 =4 which equals x² + y² -8x + 6y +21 = 0 When Three Points Are Known When you are given three points not in a straight line for example,   (9, 2)   (3, -4)   and   (5, -6) click here to see the procedure for generating the circle's equation.