ARC TO CHORD RATIO

_______________________________
Arc ÷ Chord Ratio
_______________________________

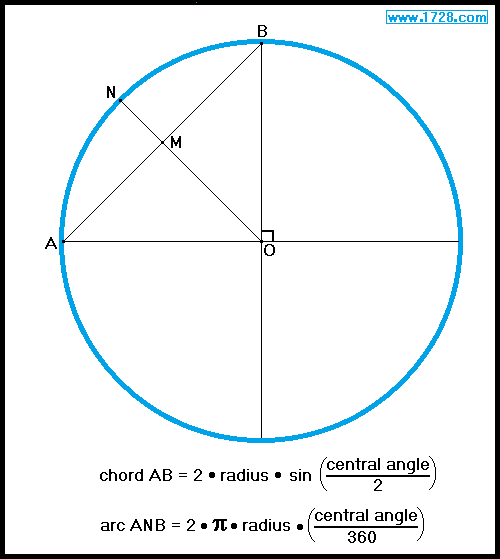
You are probably quite familiar with the formula for determining the circumference of a circle:

circumference = 2 • p • radius
If we wanted to determine the length of a portion of the circumference (what is known as an arc) then the formula is:
arc length = 2 • p • radius • (central angle ÷ 360)
If we drew a straight line from point A to point B (what is known as a chord) then the formula for the chord length is:

chord length = 2 • radius • sine (central angle ÷ 2)
Now let's suppose that the radius of the circle equals 100, then we can calculate the lengths of the arc and the chord as:
arc ANB length = 2 • p • 100 • (90 ÷ 360) = 157.07963267949
chord AB length = 2 • 100 • sine (90 ÷ 2) = 141.42135623731
Dividing the arc length by the chord length gives us the arc to chord ratio, which in this case equals 1.1107207345.
Whenever we have a circle whose central angle equals 90°, it will always subtend an arc and a chord whose ratio will always be 1.1107207345. For all other central angles, we have calculated this ratio for 1 through 180 degrees. If you just want a rough idea of what the arc to chord ratio is for a particular central angle is, then these tables are fine. However, if you need an exact answer, then use the calculator located here and choose the "Chord AB & Arc AB" menu option.

Arc ÷ Chord Ratio Angle

1.0000126925 1

1.0000507714 2

1.0001142407 3

1.0002031072 4

1.0003173803 5

1.0004570723 6

1.0006221981 7

1.0008127753 8

1.0010288241 9

1.0012703678 10

1.0015374321 11

1.0018300456 12

1.0021482395 13

1.0024920478 14

1.0028615075 15

1.003256658 16

1.0036775418 17

1.004124204 18

1.0045966924 19

1.005095058 20

1.0056193542 21

1.0061696376 22

1.0067459673 23

1.0073484055 24

1.0079770174 25

1.0086318707 26

1.0093130364 27

1.0100205881 28

1.0107546028 29

1.0115151599 30

1.0123023423 31

1.0131162356 32

1.0139569286 33

1.0148245129 34

1.0157190836 35

1.0166407385 36

1.0175895787 37

1.0185657084 38

1.0195692351 39

1.0206002693 40

1.021658925 41

1.0227453191 42

1.0238595721 43

1.0250018077 44

1.026172153 45

1.0273707383 46

1.0285976976 47

1.0298531682 48

1.0311372908 49

1.0324502098 50

1.0337920731 51

1.0351630322 52

1.0365632421 53

1.0379928618 54

1.0394520537 55

1.0409409841 56

1.0424598231 57

1.0440087448 58

1.0455879268 59

1.0471975512 60

Arc ÷ Chord Ratio Angle

1.0488378036 61

1.050508874 62

1.0522109562 63

1.0539442484 64

1.0557089529 65

1.0575052762 66

1.0593334293 67

1.0611936274 68

1.0630860903 69

1.0650110421 70

1.0669687116 71

1.0689593321 72

1.0709831418 73

1.0730403835 74

1.0751313048 75

1.0772561584 76

1.0794152016 77

1.0816086972 78

1.0838369128 79

1.0861001212 80

1.0883986007 81

1.0907326349 82

1.0931025126 83

1.0955085283 84

1.0979509823 85

1.1004301803 86

1.102946434 87

1.1055000609 88

1.1080913846 89

1.1107207345 90

1.1133884467 91

1.116094863 92

1.1188403321 93

1.121625209 94

1.1244498553 95

1.1273146394 96

1.1302199365 97

1.1331661289 98

1.1361536059 99

1.1391827639 100

1.142254007 101

1.1453677464 102

1.1485244013 103

1.1517243983 104

1.1549681721 105

1.1582561656 106

1.1615888295 107

1.1649666232 108

1.1683900145 109

1.1718594799 110

1.1753755047 111

1.1789385831 112

1.1825492187 113

1.1862079244 114

1.1899152225 115

1.1936716452 116

1.1974777346 117

1.2013340428 118

1.2052411323 119

1.2091995762 120

Arc ÷ Chord Ratio Angle

1.2132099582 121

1.217272873 122

1.2213889267 123

1.2255587364 124

1.2297829313 125

1.2340621521 126

1.2383970519 127

1.242788296 128

1.2472365626 129

1.2517425427 130

1.2563069404 131

1.2609304733 132

1.2656138731 133

1.2703578851 134

1.2751632693 135

1.2800308003 136

1.2849612677 137

1.2899554765 138

1.2950142473 139

1.3001384169 140

1.3053288385 141

1.3105863818 142

1.315911934 143

1.3213063997 144

1.3267707014 145

1.3323057802 146

1.3379125956 147

1.3435921268 148

1.3493453724 149

1.3551733512 150

1.3610771026 151

1.3670576873 152

1.3731161873 153

1.3792537072 154

1.3854713739 155

1.3917703377 156

1.3981517726 157

1.4046168773 158

1.4111668751 159

1.4178030152 160

1.4245265729 161

1.4313388505 162

1.438241178 163

1.4452349135 164

1.4523214442 165

1.4595021871 166

1.4667785899 167

1.4741521313 168

1.4816243224 169

1.4891967073 170

1.4968708638 171

1.5046484046 172

1.5125309781 173

1.5205202694 174

1.5286180011 175

1.5368259346 176

1.5451458709 177

1.553579652 178

1.5621291616 179

1.5707963268 180

_____________________

Return To Home Page
Copyright © 1999 - 1728 Software Systems