MUSIC   FREQUENCIES
The diagram above shows an 88 key piano keyboard.

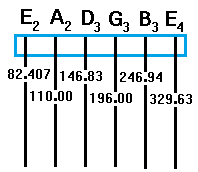
The diagram above shows the open string
notes and frequencies (Hz) of a guitar.

 Semi-
 tones 		  Note   Freq
  (Hz) 		 Semi-
 tones 		  Note   Freq
  (Hz) 		 Semi-
 tones 		  Note     Freq
    (Hz) 		 Semi-
 tones 		  Note     Freq
    (Hz)
  0   A0     27.500   0   A2     110.00   0   A4     440.00   0   A6     1,760.00
  1   B♭0     29.135   1   B♭2     116.54   1   B♭4     466.16   1   B♭6     1,864.66
  2   B0     30.868   2   B2     123.47   2   B4     493.88   2   B6     1,975.53
  3   C1     32.703   3   C3     130.81   3   C5     523.25   3   C7     2,093.00
  4   C♯1     34.648   4   C♯3     138.59   4   C♯5     554.37   4   C♯7     2,217.46
  5   D1     36.708   5   D3     146.83   5   D5     587.33   5   D7     2,349.32
  6   E♭1     38.891   6   E♭3     155.56   6   E♭5     622.25   6   E♭7     2,489.02
  7   E1     41.203   7   E3     164.81   7   E5     659.26   7   E7     2,637.02
  8   F1     43.654   8   F3     174.61   8   F5     698.46   8   F7     2,793.83
  9   F♯1     46.249   9   F♯3     185.00   9   F♯5     739.99   9   F♯7     2,959.96
  10   G1     48.999   10   G3     196.00   10   G5     783.99   10   G7     3,135.96
  11   G♯1     51.913   11   G♯3     207.65   11   G♯5     830.61   11   G♯7     3,322.44
  12   A1     55.000   12   A3     220.00   12   A5     880.00   12   A7     3,520.00
  1   B♭1     58.270   1   B♭3     233.08   1   B♭5     932.33   1   B♭7     3,729.31
  2   B1     61.735   2   B3     246.94   2   B5     987.77   2   B7     3,951.07
  3   C2     65.406   3   C4     261.63   3   C6     1,046.50   3   C8     4,186.01
  4   C♯2     69.296   4   C♯4     277.18   4   C♯6     1,108.73   **   *****     *****
  5   D2     73.416   5   D4     293.66   5   D6     1,174.66   **   *****     *****
  6   E♭2     77.782   6   E♭4     311.13   6   E♭6     1,244.51   **   *****     *****
  7   E2     82.407   7   E4     329.63   7   E6     1,318.51   **   *****     *****
  8   F2     87.307   8   F4     349.23   8   F6     1,396.91   **   *****     *****
  9   F♯2     92.499   9   F♯4     369.99   9   F♯6     1,479.98   **   *****     *****
  10   G2     97.999   10   G4     392.00   10   G6     1,567.98   **   *****     *****
  11   G♯2     103.83   11   G♯4     415.30   11   G♯6     1,661.22   **   *****     *****
  12   A2     110.00   12   A4     440.00   12   A6     1,760.00   **   *****     *****

In order to explain the table of data (above), we created yet another table (below).
The "semi-tones" column runs from zero to twelve, starting with "A" as "zero".
(We based these tables on "A440" because that is the defined frequency for western music.)
You may use the table below to determine the name of a musical interval.
For example, in the table below, going 7 semi-tones from A to E is a musical interval of a "perfect fifth".

  Semi-
  tones		   Note   Musical Interval Name
    0   A   — — — — —
 
    1   B♭   Half Step or
  Semitone
    2   B   Full Step or
  Whole Tone
    3   C   Minor
  Third
    4   C♯   Major
  Third
    5   D   Perfect
  Fourth
    6   E♭   Augmented Fourth or
  Diminished Fifth or
  Tritone
    7   E   Perfect
  Fifth
    8   F   Minor
  Sixth
    9   F♯   Major
  Sixth
    10   G   Minor
  Seventh
    11   G♯   Major
  Seventh
    12   A  
  Octave
 


The musical notes in this article are written in scientific pitch notation in which the note is designated by a letter followed by the octave it is in. So, for example, the note middle C is written as C4.

In the diagrams of musical notes above, when a note has more than one name, we only listed one of the 2 possible names. For example, we could have referred to the note B♭0 as   "A♯0 / B♭0"   but we determined that the chart is much easier to read when we give just one name to each musical note.
To help you out, here are the five pairs of notes with more than one name:

  B♭ = A♯   C♯ = D♭   E♭ = D♯   F♯ = G♭   G♯ = A♭

Music must be based on a mutually-agreed-upon standard frequency and the music of western civilization is based on "A" above middle "C" which has been defined by the International Organization for Standardization to be a musical frequency of 440 Hertz or 440 cycles per second.

Musical frequencies are based on the 12th root of two which equals 1.05946309... and a semitone's frequency equals the difference of 2 adjacent notes.
There are 12 pairs of adjacent notes:

 A & B♭    B♭ & B    B & C    C & C♯   C♯ & D   D & E♭    E♭ & E    E & F    F & F♯    F♯ & G    G & G♯    G♯ & A  

Looking at the piano diagram at the top of this page, there are no black keys between 'B & C' and 'E & F'.
Therefore, you will never see notes called B♯ C♭ E♯ or F♭

The names of musical notes repeat themselves after 12 semitones or what is called an octave.
For example the note A0 sounds exactly the same as A1 except that A1 sounds "higher" than A0. This is called octave equivalence. You may also have noticed that when notes are an octave apart, the higher note has a frequency that is exactly twice the lower frequency.
For example the frequency of A1 is 55.0 Hertz and the frequency of A0 is 27.5 Hertz and

55.0 ÷ 27.5 = 2



Return To Home Page

Copyright © 1999 -     1728 Software Systems