QUADRILATERALS

Q u a d r i l a t e r a l s Scroll to the bottom for a listing of
properties for all types of quadrilaterals

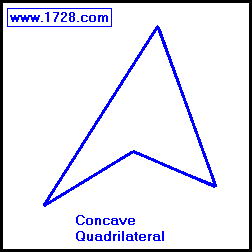A quadrilateral is a geometric figure having four sides and four angles which always total 360°.

We will discuss all types of quadrilaterals except the concave quadrilateral. (See diagram).

This type of quadrilateral has one angle greater than 180°. (Angles greater than 180° are called concave angles). These quadrilaterals are not discussed much in a typical geometry course and are not among the quadrilaterals with which you are familiar.

Generally, all a quadrilateral needs to be classified as such is four sides. However, there are six specific quadrilaterals that are worth discussing in detail.

Trapezoids
Click here for a trapezoid calculator.

First, it is important to state the difference in definitions between British and American usage.
The British use the term trapezoid to refer to a quadrilateral with no parallel sides and a trapezium is a quadrilateral with two parallel sides.

The American usage is the exact opposite of the British usage: trapezoid - two parallel sides trapezium - no parallel sides.

The only requirement for a trapezoid (American definition) is that two sides are parallel.

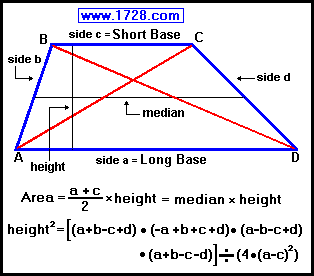Side a and side c are the parallel sides and are called bases.

The non-parallel sides (side b and side d) are called legs.

Lines AC and BD are the diagonals.

The median is perpendicular to the height and bisects lines AB and CD.

∠ A plus ∠ B = 180° ∠ C plus ∠ D = 180°

Trapezoid Area = ½ • (sum of the parallel sides) • height

height² = [(a +b -c +d) • (-a +b +c +d) • (a -b -c +d) • (a +b -c -d)] ÷ (4 • (a -c)²)

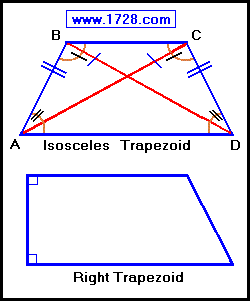Two special cases of trapezoid are worth mentioning.

The legs and diagonals of an isosceles trapezoid are equal.
AB = CD and AC = BD

Both pairs of base angles are equal
∠ A = ∠ D and ∠ B = ∠ C

The right trapezoid has two right angles.

Kites
Click here for a kite calculator.

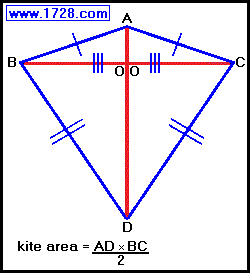∠ A and ∠ D are vertex angles

∠ B = ∠ C and are the non-vertex angles

Lines AD and BC are diagonals and always meet at right angles.

Diagonal AD is the axis of symmetry and bisects diagonal BC, bisects ∠ A and ∠ D, and bisects the kite into two congruent, triangles. (△ ABD and △ ACD)

Diagonal BC bisects the kite into two isosceles triangles. (△ ABC and △ BCD)

Side AB = side AC, side BD = side CD and Line OB = Line OC

Parallelograms
Click here for a parallelogram calculator.

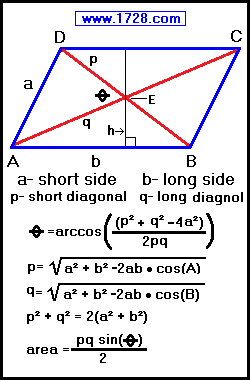• Both pairs of opposite sides are equal. (Side AD = BC Side AB = DC)
• Both pairs of opposite angles are equal (∠ A = ∠ C ∠ D = ∠ B)
• Diagonals bisect each other. AE = EC DE = EB
• Each diagonal forms two congruent triangles.
Diagonal AC forms △ ADC and △ ABC
Diagonal DB forms △ DCB and △ DAB
• Diagonals are not equal.
• Diagonals do not bisect the vertex angles.
• Area = side b • height or area = Line AB • height
• Angle A = arc sine (height ÷ side a)
• Angle A = arc cosine (side a² + side b² -p²) ÷ (2 • side a • side b)
• Angle B = (180° -Angle A)
• Side a = Square Root [ (p² + q² -2b²) / 2 ]
• Side b = Square Root [ (p² + q² -2a²) / 2 ]
• Height = side a • sine (A)
• Perimeter = 2 • (side a + side b)

Rhombuses
Click here for a rhombus calculator.

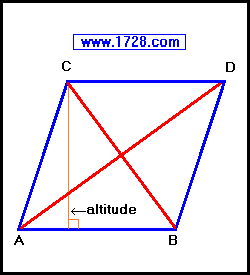• All four sides are equal (Side AB = BD = DC = CA)
• Diagonals meet at right angles
• Diagonals bisect each other
• Diagonals bisect the vertex angles ∠ A ∠ B ∠ C and ∠ D
• Both pairs of opposite angles are equal
∠ A = ∠ D ∠ C = ∠ B
• Adjacent angles are supplementary (they sum to 180°)
∠ A + ∠ B = ∠ B + ∠ D = ∠ D + ∠ C = ∠ C + ∠ A = 180°
• Rhombus Altitude = side • sine (either angle) = (AD • CB) ÷ (2 • side)
• Rhombus Area = (AD × CB) ÷ 2 = side • altitude = side² • sine (either angle)
• Long Diagonal AD = Side Length • Square Root [ 2 + 2 • cos(A) ]
• Short Diagonal BC = Side Length • Square Root [ 2 + 2 • cos(B) ]
• 4 • Side² = Long Diagonal² + Short Diagonal²

Rectangles
Click here for a rectangle and square calculator.

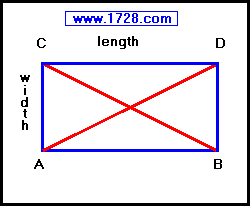• Opposite sides are parallel and equal

• All 4 angles are right angles

• Diagonals bisect each other and are equal

• Rectangle Area = length × width

• Perimeter = (2 × length) + (2 × width)

Squares
Click here for a rectangle and square calculator.

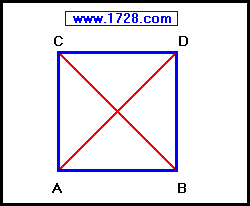• All 4 sides are equal

• All 4 angles are right angles

• Diagonals bisect each other at right angles and are equal

• Perimeter = 4 × side length

• Area = (side length)²

Quadrilateral Properties


D I A G O N A L S	Isosceles Trapezoid	Kite	Parallel ogram	Rhombus	Rectangle	Square
Diagonals Bisect Each Other			Y E S	Y E S	Y E S	Y E S
Diagonals Are Equal	Y E S				Y E S	Y E S
Diagonals Meet At Right Angles		Y E S		Y E S		Y E S
P A R A L L E L S I D E S	Isosceles Trapezoid	Kite	Parallel ogram	Rhombus	Rectangle	Square
Only 2 Sides Are Parallel	Y E S
No Sides Are Parallel		Y E S
Both Pairs of Opposite Sides Are Parallel			Y E S	Y E S	Y E S	Y E S
E Q U A L S I D E S	Isosceles Trapezoid	Kite	Parallel ogram	Rhombus	Rectangle	Square
Only 2 Sides Are Equal	Y E S
Both Pair of Adjacent Sides Are Equal But No Opposite Sides Are Equal		Y E S
Both Pair of Opposite Sides Are Equal			Y E S	Y E S	Y E S	Y E S
All Four Sides Are Equal				Y E S		Y E S
A N G L E S	Isosceles Trapezoid	Kite	Parallel ogram	Rhombus	Rectangle	Square
Both Pairs of Base Angles Are Equal	Y E S
Non-Vertex Angles Are Equal		Y E S
Only Opposite Angle Pairs Are Equal			Y E S	Y E S
All Four Angles Are Right Angles					Y E S	Y E S
O T H E R	Isosceles Trapezoid	Kite	Parallel ogram	Rhombus	Rectangle	Square
Cyclic Quadrilateral	Y E S				YES	YES
Tangential Quadrilateral		YES		YES		YES

A circle can be circumscribed around a cyclic quadrilateral and its opposite angles add up to 180°

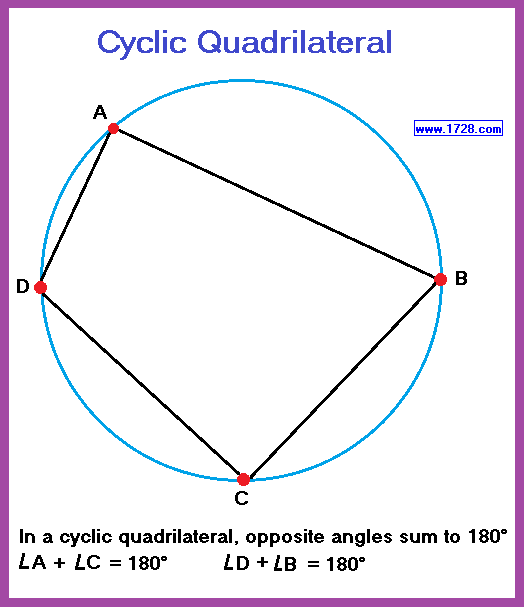
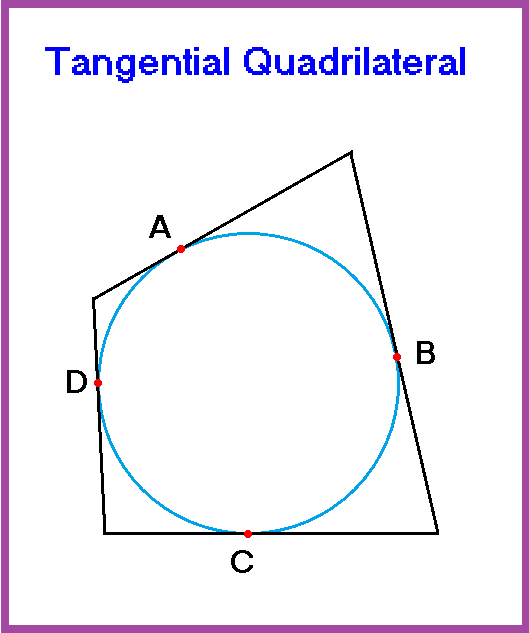
A circle can be inscribed inside a tangential quadrilateral.

Return To Home Page